Demostración matemática del método de los dos vatímetros para medir la potencia de un sistema trifásico. Aplicación para medida de potencia reactiva en sistemas equilibrados.
Introducción
Los sistemas trifásicos tienen particularidades respecto a sistemas monofásicos o de más fases. Desde el punto de vista técnico transmiten el triple de energía que un sistema monofásico con solo añadir un cable, por tanto desde el punto de vista económico resultan muy atractivos. Matemáticamente también presentan algunas curiosidades, cómo medir la potencia reactiva de un sistema equilibrado mediante un vatímetro o la potencia total de las tres fases con solo dos.
Aunque el uso de vatímetros analógicos parezca de otra época, analizar sus posibilidades abre el camino a implementaciones modernas igual de curiosas. Por ejemplo, en muchos convertidores de potencia para generadores de inducción doblemente alimentados, solo se monitorizan dos fases en el lado del rotor, e incluso, en el lado de línea. ¿Lo hacen por priorizar ahorro sobre calidad o hay otro motivo?
Método de los tres vatímetros
Entender primero el método de los tres vatímetros tiene su razón académica, ya que el de los dos vatímetros sería un caso particular de este. Se supone un sistema trifásico que no tiene porque estar equilibrado con tensiones de fase u1, u2 y u3 conectado a una carga trifásica de impedancias Z1, Z2 y Z3 y cuyo neutro N no tiene porqué ser accesible. Se intercalan tres vatímetros iguales conectándose a una referencia común que se denominará Nw, así, los vatímetros forman una carga trifásica equilibrada.
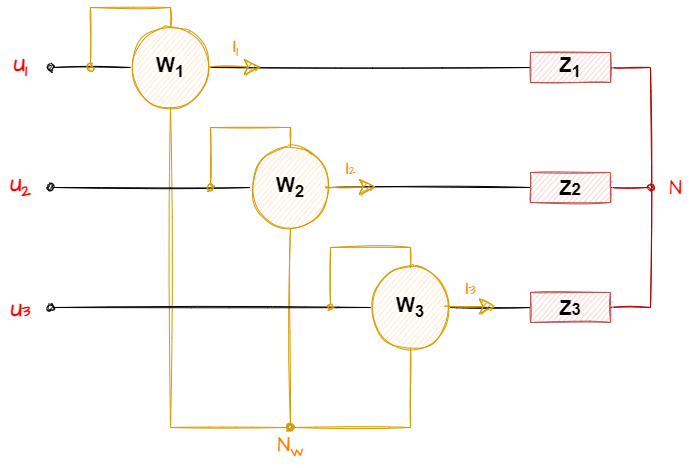
La suma de las medidas de los vatímetros será
\[W_1+W_2+W_3=\mathbb{R}\{\overline{U_{1N_w}}·\overline{I_1^*} + \overline{U_{2N_w}}·\overline{I_2^*} + \overline{U_{3N_w}}·\overline{I_3^*}\}\quad(1)\]
Donde \[\mathbb{R}\{…\}\] es la parte real del número complejo resultante de la suma. La diferencia de tensión entre las fases y el neutro de los vatímetros es \[\overline{U_{1N_w}},\overline{U_{2N_w}},\overline{U_{3N_w}}\] por último \[ \overline{I_1^*},\overline{I_2^*},\overline{I_3^*}\] son los conjugados de las intensidades de línea.
Con la segunda Ley de Kirchhoff se plantean las siguientes ecuaciones\[
\left.
\begin{array}{rcl}
\overline{U_{1N}}&=&\overline{U_{1N_w}}+\overline{U_{N_wN}}
\\ \overline{U_{2N}}&=&\overline{U_{2N_w}}+\overline{U_{N_wN}}
\\ \overline{U_{3N}}&=&\overline{U_{3N_w}}+\overline{U_{N_wN}}
\end{array}
\right\}\quad(2)\]
Despejando en (2) las tensiones en los vatímetros y sustituyéndolos en (1) se tiene
\[W_1+W_2+W_3=\mathbb{R}\left\lbrace
(\overline{U_{1N}}-\overline{U_{N_wN}})·\overline{I_1^*}+
(\overline{U_{2N}}-\overline{U_{N_wN}})·\overline{I_2^*}+
(\overline{U_{3N}}-\overline{U_{N_wN}})·\overline{I_3^*}\right\rbrace
\]
Operando
\[W_1+W_2+W_3=\mathbb{R}\left\lbrace
\overline{U_{1N}}·\overline{I_1^*}+\overline{U_{2N}}·\overline{I_2^*}+\overline{U_{3N}}·\overline{I_3^*}
-\overline{U_{N_wN}}(\overline{I_1^*}+\overline{I_2^*}+\overline{I_3^*})\right\rbrace
\]
Podemos analizar la ecuación anterior en dos partes, la primera
\[\overline{U_{1N}}·\overline{I_1^*}+\overline{U_{2N}}·\overline{I_2^*}+\overline{U_{3N}}·\overline{I_3^*}\]
coincide con la potencia total absorbida por la carga trifásica. Por tanto, para que la suma de las indicaciones de los vatímetros coincida con dicha potencia, la segunda parte \[-\overline{U_{N_wN}}(\overline{I_1^*}+\overline{I_2^*}+\overline{I_3^*})\] debe anularse. Esto ocurre en dos situaciones
- El neutro de la carga se encuentra aislado, por tanto la suma de las corrientes es cero (primera ley de Kirchhoff).
- Existe hilo neutro pero la corriente que circula por él es nula.
En resumen
\[\overline{I_1^*}+\overline{I_2^*}+\overline{I_3^*}=0\quad(3)\]
Método de los dos vatímetros
Entendido el método de los tres vatímetros, se puede apreciar la siguiente «curiosidad» al representar los fasores de las tensiones.
En la siguiente imagen se muestra en forma fasorial un sistema de tensiones trifásico balanceado. Se han representado en rojo las tensiones de fase y en azul las tensiones de línea, con el neutro N como origen de todos los fasores. Bajo la misma imagen se representa el mismo sistema, pero colocando los fasores de las tensiones de línea de una forma más particular: un triángulo.
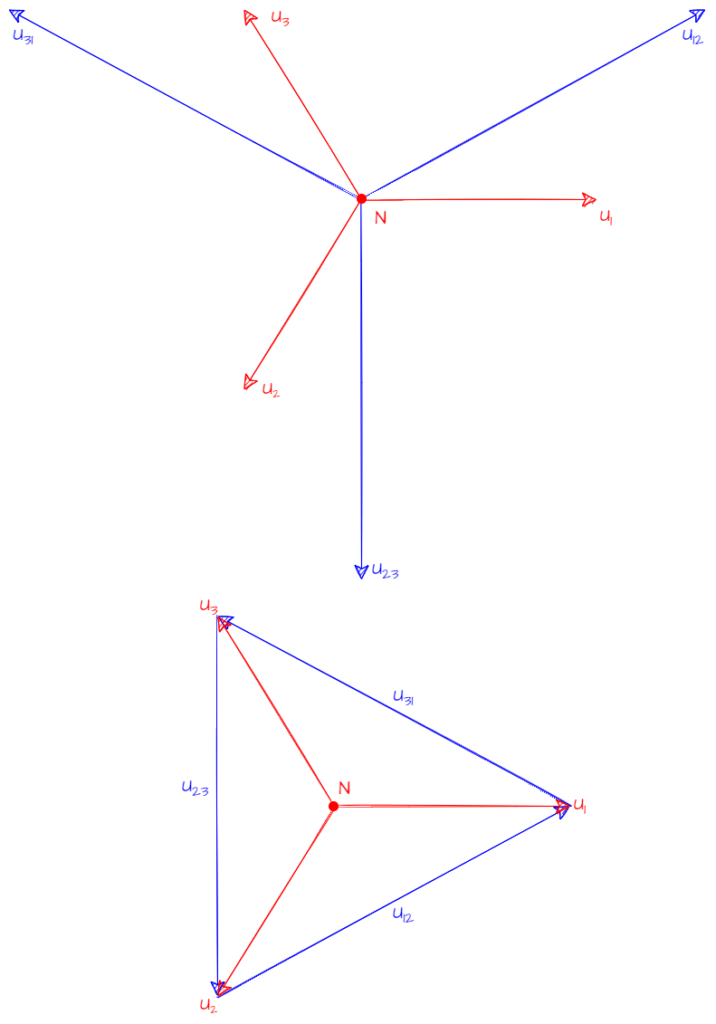
Cuando el sistema de tensiones está equilibrado el neutro se ubica en el baricentro del triángulo, el cual coincidiría también con el centro de la circunferencia circunscrita a este. El punto neutro es la clave del método de los dos vatímetros ¿Qué ocurre al desplazar N a un vértice del triángulo?
Para mover el punto N de la imagen anterior a uno de los vértices basta con conectar las referencias de los tres vatímetros a una de las fases, como se muestra a continuación.

La indicación de W3 será cero al ser la tensión medida nula, por tanto, el vatímetro puede retirarse, para los otros dos se tiene que
\[W_1+W_2=\mathbb{R}\{\overline{U_{13}}·\overline{I_1^*}+\overline{U_{23}}·\overline{I_2^*}\}\]
Donde las tensiones de línea U13 y U23 pueden sustituirse aplicando Kirchhoff por U1N+UN3 y U2N+UN3, respectivamente. Por tanto
\[W_1+W_2=\mathbb{R}\{
(\overline{U_{1N}}+\overline{U_{N3}})·\overline{I_1^*}+
(\overline{U_{2N}}+\overline{U_{N3}})·\overline{I_2^*}\}\]
\[W_1+W_2=\mathbb{R}\{
\overline{U_{1N}}·\overline{I_1^*}+
\overline{U_{2N}}·\overline{I_2^*}+
\overline{U_{N3}}·(\overline{I_1^*}+\overline{I_2^*})\}\]
Como la suma de las intensidades es cero (3), se puede sustituir el último término de la ecuación anterior de la siguiente manera
\[W_1+W_2=\mathbb{R}\{
\overline{U_{1N}}·\overline{I_1^*}+
\overline{U_{2N}}·\overline{I_2^*}+
\overline{U_{N3}}·(-\overline{I_3^*})\}\]
\[W_1+W_2=\mathbb{R}\{
\overline{U_{1N}}·\overline{I_1^*}+
\overline{U_{2N}}·\overline{I_2^*}+
\overline{U_{3N}}·\overline{I_3^*}\}\]
De nuevo la suma de las indicaciones de los vatímetros coincide con la potencia total de la carga trifásica. Sin embargo, esta vez se ha utilizado un vatímetros menos.
Método de los dos vatímetros en sistemas equilibrados. Medida de reactiva
Todo lo desarrollado hasta ahora es válido siempre que se cumpla (3), sin importar que las tensiones o la carga estén o no equilibradas. Para el siguiente desarrollo se supondrá que el sistema es equilibrado y además que
- Tensiones de línea U13 = U23 = = U31 = UL
- Secuencia directa
- Intensidades de línea Ia = Ib = Ic = IL
- Carga inductiva ϕ
Cada vatímetro, realizaría las siguientes medidas
\[\left.
\begin{array}{rcl}
W_1&=&\mathbb{R}\{\overline{U_L}·\overline{I_L^*}\}=U_L·I_L·\cos(\theta_{U_{13}}-\theta_{I_1})
\\ W_2&=&\mathbb{R}\{\overline{U_L}·\overline{I_L^*}\}=U_L·I_L·\cos(\theta_{U_{23}}-\theta_{I_2})
\end{array}
\right\}\quad donde \]
\[\left.
\begin{array}{rcl}
\theta_{U_{13}}&\rightarrow& \text{Desfase tensión }U_{13}
\\ \theta_{U_{23}}&\rightarrow& \text{Desfase tensión }U_{23}
\\ \theta_{I_{1(y)2}}&\rightarrow& \text{Desfase intensidad }\varphi
\end{array}
\right\}\]
El diagrama fasorial del sistema planteado es el siguiente, nótese que las dos tensiones de fase y la de línea forman un triángulo isósceles.
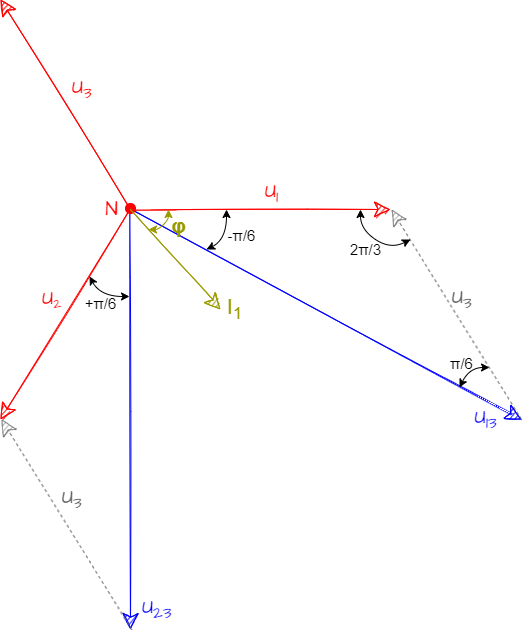
\[\begin{array}{rcl}
\theta_{U_{13}}-\theta_{I_1}&=& \frac{-\pi}{6}+\varphi
\\ \theta_{U_{23}}-\theta_{I_2}&=& \frac{\pi}{6}+\varphi
\end{array}\]
De esta manera se tiene
\[\left.
\begin{array}{rcl}
W_1&=&U_L·I_L·\cos\left(\frac{-\pi}{6}+\varphi\right)
\\ W_2&=&U_L·I_L·\cos\left(\frac{\pi}{6}+\varphi\right)
\end{array}
\right\}\]
Aplicando las identidades trigonométricas de suma y diferencia de ángulos
\[\left.
\begin{array}{rcl}
W_1&=&U_L·I_L·\cos(\frac{\pi}{6})·\cos(\varphi)&+&U_L·I_L·\sin(\frac{\pi}{6})·\sin(\varphi)
\\ W_2&=&U_L·I_L·\cos(\frac{\pi}{6})·\cos(\varphi)&-&U_L·I_L·\sin(\frac{\pi}{6})·\sin(\varphi)
\end{array}
\right\}\]
La suma y diferencia de las lecturas son
\[\left.
\begin{array}{rcl}
W_1+W_2&=&2·U_L·I_L·\cos(\frac{\pi}{6})·\cos(\varphi)
\\ W_1-W_2&=&2·U_L·I_L·\sin(\frac{\pi}{6})·\sin(\varphi)
\end{array}
\right.\]
Sustituyendo
\[\cos\left(\frac{\pi}{6}\right)=\frac{\sqrt{3}}{2}\quad ; \quad \sin\left(\frac{\pi}{6}\right)=\frac{1}{2}\]
Finalmente se tiene
\[\left.
\begin{array}{rcl}
W_1+W_2&=&\sqrt{3}·U_L·I_L·\cos(\varphi)
\\ W_1-W_2&=&U_L·I_L·\cos(\varphi)
\end{array}
\right.\]
Recordando que
\[U_L=\sqrt{3}·U_F \quad ; \quad I_L=I_F\]
Se tiene (como era de esperar por la conclusión del método de los tres vatímetros) que la suma de las indicaciones de los dos vatímetros equivale a la potencia total.
\[W_1+W_2=3·U_F·I_F·\cos(\varphi)=P_T\]
Por otro lado, la potencia reactiva puede obtenerse de la diferencia de la siguiente forma
\[Q_T=\sqrt{3}·U_L·I_L·\sin(\varphi)=\sqrt{3}(W_1-W_2)\]
Es posible repetir las deducciones para secuencia de fases inversa y cargas capacitivas, mientras que la potencia total nunca varía, el signo de la energía reactiva variará, por ejemplo para el caso desarrollado pero con secuencia inversa de fases la energía reactiva será
\[Q_T=-\sqrt{3}(W_1-W_2)\]
El resumen de los signos para interpretar la lectura de los vatímetros y la energía reactiva se muestra en la siguiente tabla.
| W1-W2 | Secuencia directa | Secuencia inversa |
|---|---|---|
| Carga inductiva | + | – |
| Carga capacitiva | – | + |