Diagramas de Bode con Octave

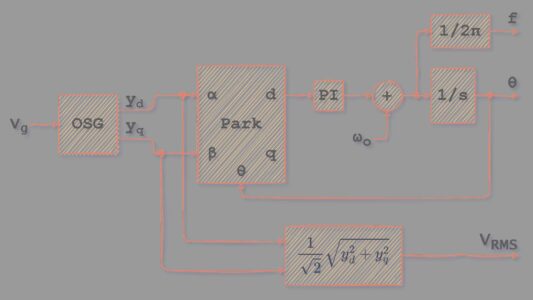
Recopilación de trucos y métodos más habituales para trazar diagramas de Bode con Octave.

Realizar diagramas de Bode con Octave es sencillo siempre y cuando no se necesiten detalles específicos, es en ese punto cuando comienzan las búsquedas más o menos exitosas por internet, se pretende reunir las respuestas a las consultas más habituales.

Diagrama de Bode básico

Para las pruebas se comienza suponiendo la función de transferencia del filtro de primer orden

\[G(s)=\frac{\omega_0}{s + \omega_0}\]

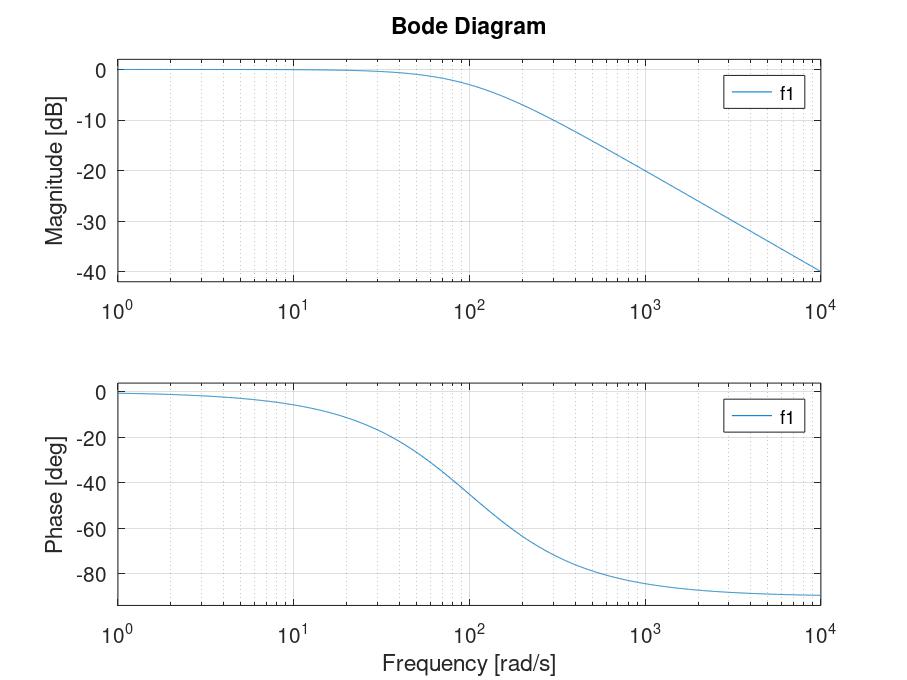
Un código como el siguiente devuelve un diagrama de Bode sencillo que sirve perfectamente para ver de forma general el comportamiento del sistema en el dominio de la frecuencia (se debe cargar el paquete control con pkg load control).

wo = 100;
f1 = tf([wo], [1 wo])
bode(f1)

Formato del trazado

El comando bode(Gs) permite modificadores sin necesidad de complicar en exceso el código mediante duplas «propiedad»-valor, estos en teoría son los mismos que plot(), sin embargo hasta al menos la versión 7.1.0 esto no es del todo cierto.

• linestyle
  • ‘-’ Línea continua (por defecto)
  • ‘–’ Línea
  • ‘:’ Línea de puntos
  • ‘-.’ Use dash-dotted lines
• marker
  • ‘+’, ‘o’, ‘*’, ‘.’, ‘x’, ‘s’, ‘d’, ‘^’, ‘v’, ‘>’, ‘<’, ‘p’, ‘h’
• linewidth (no funciona en Bode(Gs))
  • Ancho en número decimal, 1 por defecto
• markersize
  • Valores numéricos positivos
• color
  • ‘k’ negro
  • ‘r’ rojo
  • ‘g’ verde
  • ‘b’ azul
  • ‘m’ magenta
  • ‘c’ cian
  • ‘w’ blanco

Rango de análisis

Puede que el rango analizado por defecto no sea adecuado, para modificarlo se puede usar el siguiente código

wo = 100;
F = tf([wo], [1 wo])

n = 1000; %Puntos análisis frecuencia
w_i = 0;  %Frecuencia inicial 10^x
w_f = 5;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);

bode(F, rango)

El número de puntos de análisis es orientativo y depende de las necesidades de la representación, para conseguir la ilusión de continuidad es recomendable usar al menos 100 puntos/década para trazado con línea y 1000 puntos/década para trazado con puntos. En otras ocasiones, por ejemplo para comparar varios diagramas en la misma gráfica, se pueden cambiar los marcadores entre ellas necesitando menos de 20 puntos/década.

Mostrar frecuencia en hercios

Algo habitual puede ser mostrar la frecuencia del eje x en hercios (Hz) en lugar de radianes/segundo (rad/s), hay un método muy simple trabajando con los datos del diagrama una vez se ha generado. En cualquier caso, la función de transferencia trabajará en rad/s, debe tenerse en cuenta para evitar el error habitual de generarlas pasando una frecuencia en hercios.

wo = 100;
F = tf([wo], [1 wo])
bode(F)

XdataObjs = findobj(gcf,'-property','XData');
set(XdataObjs(2), 'XData', get(XdataObjs(2),'XData')/(2*pi));
set(XdataObjs(4), 'XData', get(XdataObjs(4),'XData')/(2*pi));
xlabel('Frequency (Hz)');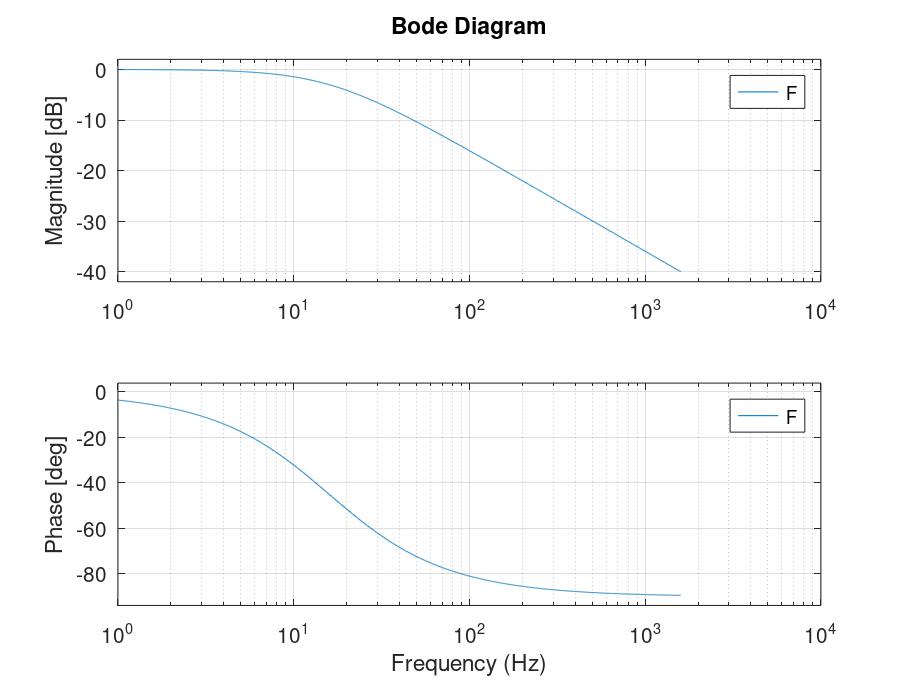

Sin embargo, este método no es muy recomendable ya que no permite mucha flexibilidad y la posición de los objetos puede variar. Para realizar manipulaciones en un diagrama de Bode lo más recomendable es extraer los datos del mismo a matrices, operar sobre esas matrices y luego pintar los datos como se desee con el comando semilogx() (en el que si funcionan correctamente los modificadores), para ello se puede utilizar un código como el siguiente

wo = 100;
F = tf([wo], [1 wo])

[mag, pha, w] = bode(F);

mag = 20*log10(mag);
w = w/(2*pi());

subplot(2, 1, 1)
semilogx(w, mag)
grid on
ylabel("Ganancia (dB)")
xlabel("Frecuencia (Hz)")

subplot(2, 1, 2)
semilogx(w, pha)
grid on
ylabel("Fase (°)")
xlabel("Frecuencia (Hz)")

Por último, para que el diagrama no aparezca cortado, puede ajustarse el rango del eje x aumentando el rango de análisis y luego recortar la gráfica:

wo = 100;
F = tf([wo], [1 wo])

n = 100; %Puntos análisis frecuencia
w_i = -1;  %Frecuencia inicial 10^x
w_f = 5;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);

[mag, pha, w] = bode(F, rango);

mag = 20*log10(mag);
w = w/(2*pi());

subplot(2, 1, 1)
semilogx(w, mag)
axis([min(w), max(w), min(mag), 10])
grid on
ylabel("Ganancia (dB)")
xlabel("Frecuencia (Hz)")

subplot(2, 1, 2)
semilogx(w, pha)
axis([min(w), max(w), -90, 0])
grid on
ylabel("Fase (°)")
xlabel("Frecuencia (Hz)")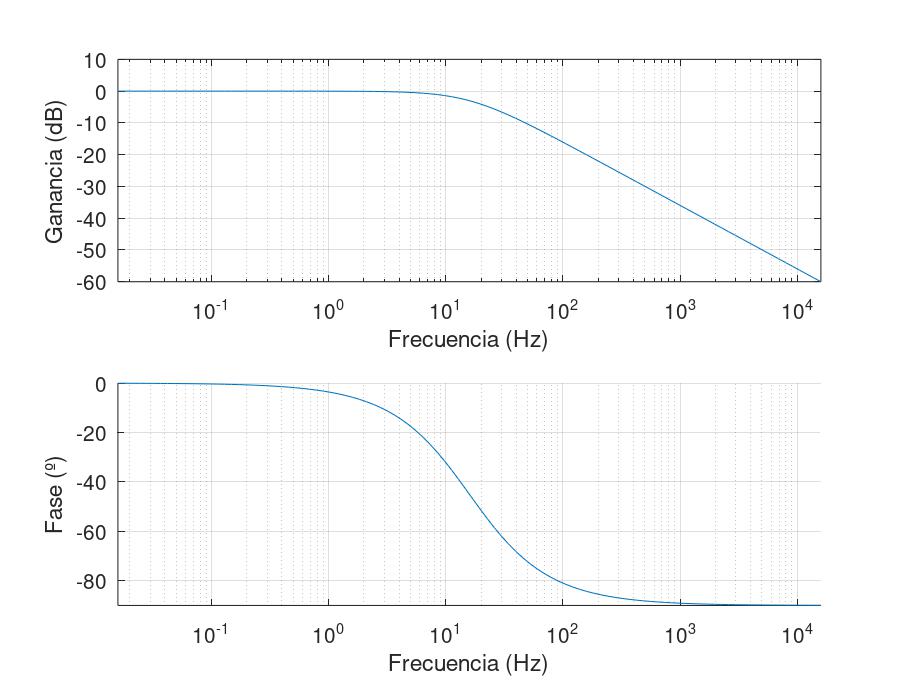

Funcionamiento comando subplot(x, y, z)

El comando subplot() permite gestionar distintas gráficas en una misma ventana generada con Octave, sus argumentos más básicos son subplot(x, y, z) donde

• x: número de filas en la ventana
• y: número de columnas en la ventana
• z: elemento a manipular, siguiendo el orden de la siguiente imagen

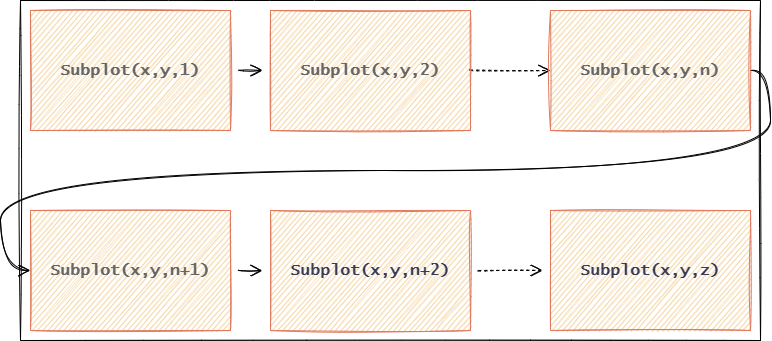
Valores por unidad

En muchas ocasiones se quiere mostrar el comportamiento de un sistema comparándolo con algún parámetro del mismo, por ejemplo, se podría querer conocer la forma del diagrama de Bode en torno a la frecuencia de corte w_o de un filtro.

Bastará dividiendo la matriz con los puntos de frecuencia entre w_o.

wo = 100;
F = tf([wo], [1 wo])

n = 100; %Puntos análisis frecuencia
w_i = -1;  %Frecuencia inicial 10^x
w_f = 5;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);

[mag, pha, w] = bode(F, rango);

mag = 20*log10(mag);
w = w/wo;

subplot(2, 1, 1)
semilogx(w, mag)
axis([min(w), max(w), min(mag), 10])
grid on
ylabel("Ganancia (dB)")
xlabel("Frecuencia (Hz)")

subplot(2, 1, 2)
semilogx(w, pha)
axis([min(w), max(w), -90, 0])
grid on
ylabel("Fase (°)")
xlabel("Frecuencia (Hz)")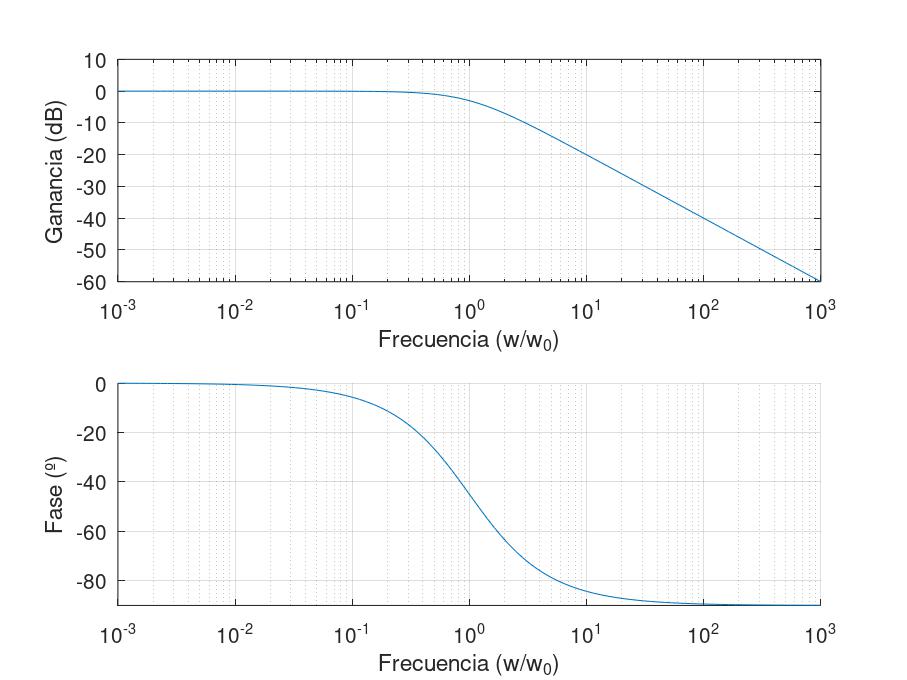

Añadir marcas a trazados

Es habitual que en un diagrama de Bode se quiera destacar una frecuencia y magnitud, en el filtro de ejemplo se podría querer destacar la frecuencia de corte, su magnitud y su desfase.

Trazar rectas con comando plot()

Se pueden trazar rectas que comienzan y finalizan en los puntos (x0, y0) y (x1, y1) con el comando plot() de la siguiente forma

plot([x0 x1], [y0 y1], «modificador», parámetro)

Añadir texto en gráficas de Octave

Para añadir un texto en las coordenadas x0, y0 se usa el comando text(), se debe recordar que todos los cambios se realizan en la última gráfica activa, por lo que podría ser necesario utilizar el comando subplot()

text(x0, y0, «texto a añadir»)

wo = 100;
F = tf([wo], [1 wo])

n = 1000; %Puntos análisis frecuencia
w_i = -1;  %Frecuencia inicial 10^x
w_f = 5;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);

[mag, pha, w] = bode(F, rango);

mag = 20*log10(mag);
w = w/wo;

subplot(2, 1, 1)
hold on
semilogx(w, mag, "marker", '.', 'r', "markersize", 10)
axis([min(w), max(w), min(mag), 10])
plot([min(w) 1], [0 0], 'k', "linestyle", '--', "linewidth", 1.1)
plot([1 max(w)], [0 min(mag)], 'k', "linestyle", '--', "linewidth", 1.1)
plot([min(w) 1], [-3 -3], 'k', "linestyle", ':', "linewidth", 1)
plot([1 1], [-3 min(mag)], 'k', "linestyle", ':', "linewidth", 1)
grid on
ylabel("Ganancia (dB)")
xlabel("Frecuencia (w/w_0)")

subplot(2, 1, 2)
hold on
semilogx(w, pha, "marker", '.', 'r', "markersize", 10)
axis([min(w), max(w), -90, 0])
plot([min(w) 0.1], [0 0], 'k', "linestyle", '--', "linewidth", 1.1)
plot([0.1 10], [0 -90], 'k', "linestyle", '--', "linewidth", 1.1)
plot([10 max(w)], [-90 -90], 'k', "linestyle", '--', "linewidth", 1.1)
plot([min(w) 1], [-45 -45], 'k', "linestyle", ':', "linewidth", 1)
plot([1 1], [-45 -90], 'k', "linestyle", ':', "linewidth", 1)
grid on
ylabel("Fase (°)")
xlabel("Frecuencia (w/w_0)")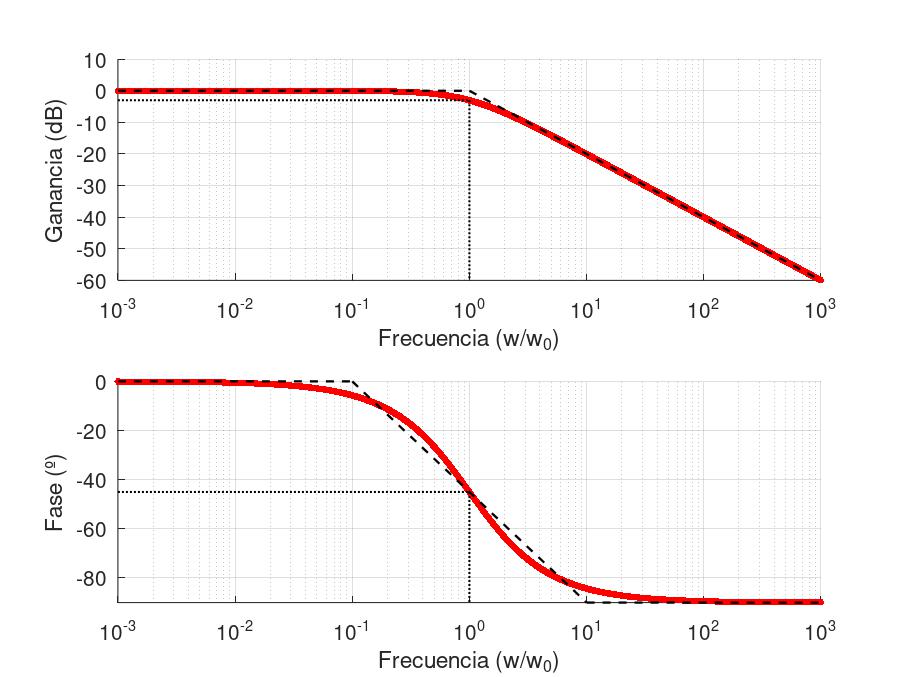

Trazado difuminado en diagramas de Bode con Octave

Aunque se trabajen con funciones de transferencia en tiempo continuo, se debe tener en cuenta que Octave es un software ejecutándose en una máquina digital y por tanto, en un sistema discreto. La forma en la que ciertos programas simulan el comportamiento en tiempo continuo es aumentando la frecuencia de muestreo de forma que no se noten los saltos entre una muestra y otra. Si esto es lo que hace Octave, ¿Qué tiene que ver ahora?

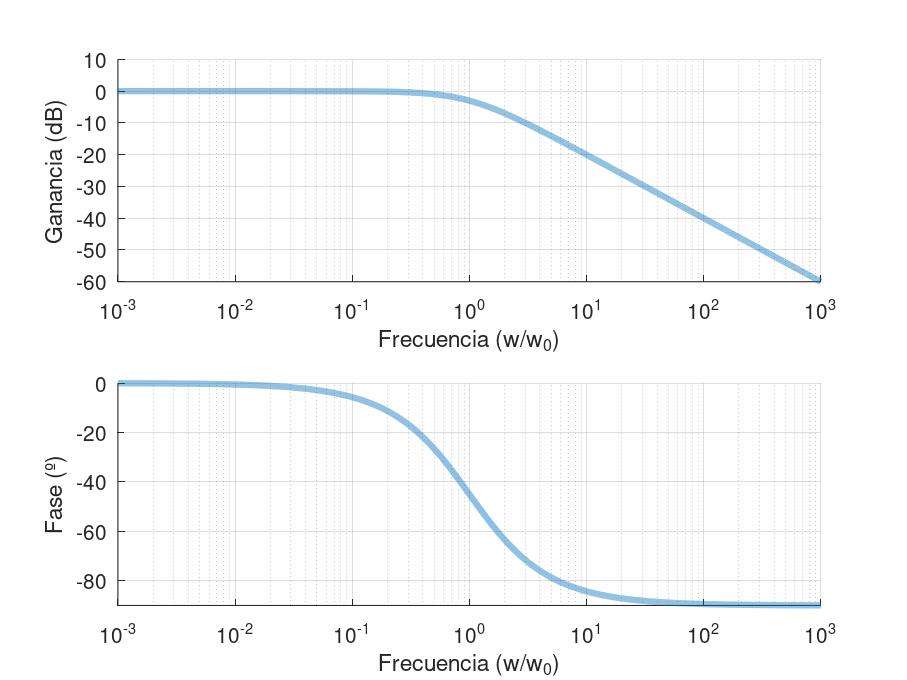
En Octave, al aumentar el grosor de un trazado cuando los puntos que lo forman están muy cerca, se produce este efecto de difuminado. Una forma de solucionarlo es decirle a Octave que utilice marcadores tipo punto mediante bode(Gs, marker ‘.’), de esta forma todos los puntos del trazado se volverán completamente sólidos.

wo = 100;
F = tf([wo], [1 wo])

n = 10000; %Puntos análisis frecuencia
w_i = -1;  %Frecuencia inicial 10^x
w_f = 5;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);

[mag, pha, w] = bode(F, rango);

mag = 20*log10(mag);
w = w/wo;

subplot(2, 1, 1)
hold on
semilogx(w, mag, "marker", '.', "markersize", 10)
axis([min(w), max(w), min(mag), 10])
grid on
ylabel("Ganancia (dB)")
xlabel("Frecuencia (w/w_0)")

subplot(2, 1, 2)
hold on
semilogx(w, pha, "marker", '.', "markersize", 10)
axis([min(w), max(w), -90, 0])
grid on
ylabel("Fase (°)")
xlabel("Frecuencia (w/w_0)")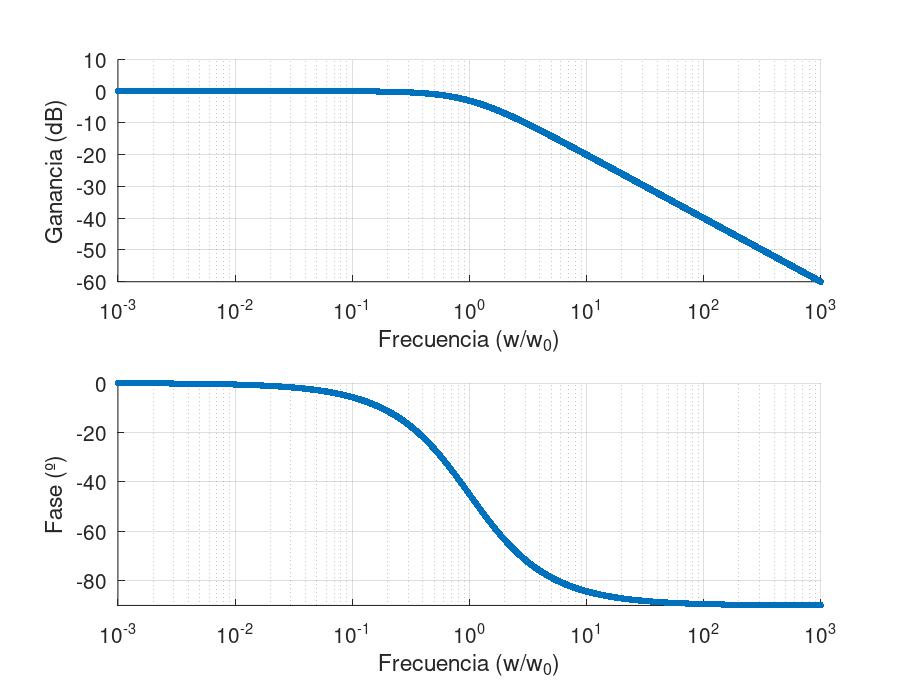

Una alternativa muy eficaz al marcador punto es el marcador ‘o’. En este caso habrá que reducir el tamaño del mismo con «markersize», 0.5 u otro valor al gusto.

Varios diagramas en la misma ventana

En el caso que sea necesario representar varios diagramas de Bode como en el caso de un sistema SOGI, donde se tienen dos respuestas distintas para una misma entrada, se necesitará colocar varios diagramas en paralelo como en la siguiente imagen

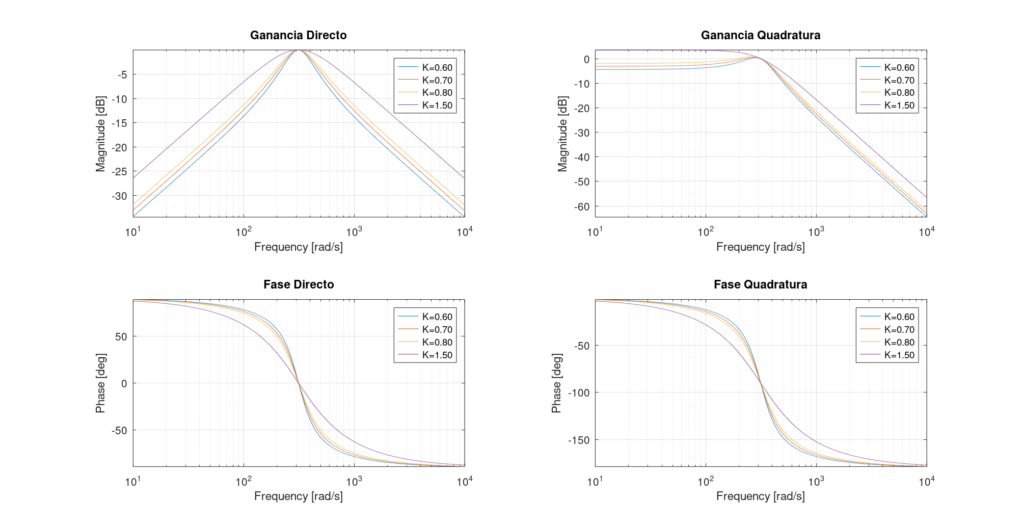
En esta imagen además de tener dos diagramas de Bode se tienen varias configuraciones para cada uno. La forma más práctica de lograr esto es mediante matrices dinámicas, así no será necesario especificar a priori el número de elementos que se trazarán en cada gráfica. El código para ello es el siguiente

clear; close all;  clc; clf;
pkg load control

wo = 2*pi*50;   %Parámetro frecuencia resonancia del SOGI
k = [0.6, 0.7, 0.8, 1.5];   %Parámetro k del SOGI

%Variables análisis
n = 1000; %Puntos análisis frecuencia
w_i = 1;  %Frecuencia inicial 10^x
w_f = 4;  %Frecuencia final 10^x
rango = logspace(w_i, w_f, n);
%Matrices resultados analisis frecuencia
d_bode = zeros(2, n, length(k)); %[mag, phas] x n x nk
q_bode = zeros(2, n, length(k)); %[mag, phas] x n x nk
mag = 1; pha = 2; %Posición de los valores en matriz

%Strings gráficas
titulos = {"Ganancia Directo";"Ganancia Quadratura";
           "Fase Directo";"Fase Quadratura"};
legend_str = cell([1 length(k)]);  %Texto para leyendas
for i=1:length(k)
  legend_str(1,i) = sprintf("K=%.2f", k(i));
endfor

%Análisis TF según k
for i=1:length(k)
  Hd=tf([k(i)*wo 0],[1 k(i)*wo wo^2]);  %TF SOGI directa
  Hq=tf([k(i)*wo^2],[1 k(i)*wo wo^2]);  %TF SOGI cuadratura
  [d_bode(mag,:,i), d_bode(pha,:,i)] = bode(Hd, rango);
  [q_bode(mag,:,i), q_bode(pha,:,i)] = bode(Hq, rango);
endfor

%Convierte magnitude a dB
for j=1:length(k)
  for i=1:n
    d_bode(mag,i,j)=20*log10(d_bode(mag,i,j));
    q_bode(mag,i,j)=20*log10(q_bode(mag,i,j));
  endfor
endfor

%Dibuja graficas
for j=1:length(k)
  hold on
  subplot(2, 2, 1)
  semilogx(rango, d_bode(mag,:,j))

  hold on
  subplot(2, 2, 2)
  semilogx(rango, q_bode(mag,:,j))

  hold on
  subplot(2, 2, 3)
  semilogx(rango, d_bode(pha,:,j))

  hold on
  subplot(2, 2, 4)
  semilogx(rango, q_bode(pha,:,j))
endfor
%Formato gráficas
for j=1:4
  subplot(2, 2, j)
  grid on
  xlabel("Frequency [rad/s]");
  legend(legend_str)
  title(titulos(j))
  axis("tight")
  if(j<3)
    ylabel("Magnitude [dB]");
  else
    ylabel("Phase [deg]");
  endif
endfor