La fase de la red eléctrica es una variable a monitorizar en aplicaciones conectadas a ella. Se introducirán varios métodos de sincronización con redes monofásicas, analizando pros y contras de cada uno.
Introducción
Las Redes Eléctricas de distribución gozan de gran robustez incluso en sistemas insulares. A pesar de ello es frecuente ver fluctuaciones incluso en sistemas continentales fuertemente mallados. Cualquier generador eléctrico (independientemente de su fuente de energía) que desee conectarse a una Red Eléctrica, no solo tiene que mantenerse sincronizado con ella, también debe soportar cambios impredecibles (de duración indeterminada) en los parámetros de la misma, como tensión o frecuencia.
De todas las formas de generación eléctrica, solo las basadas en generadores síncronos conectados directamente a Red gozan de sincronización natural, aportando más estabilidad* cuanta más inercia posee su rotor. Los generadores que transmiten su energía mediante electrónica de potencia deben forzar dicha sincronización, para lo que existen métodos como los introducidos a continuación.
*La frecuencia no es el único parámetro decisivo en una red, la regulación de tensión también es fundamental.
Detección de paso por cero
Es una técnica simple donde se evalúa si el valor de la tensión de una fase respecto al neutro es mayor o menor que cero. Es un método simple y fácil de implementar, como contra, es muy susceptible a captar ruido alterando de forma importante la frecuencia medida. La implementación de filtros e histéresis mejora los resultados, pero introducen deformaciones que deben ser compensadas.
La frecuencia de muestreo es dos veces por ciclo o periodo, suficiente en algunos casos. La principal contra será que no permite obtener información de la amplitud, algo que en la inmensa mayoría de los casos obligará a añadir dicha medida de forma paralela.
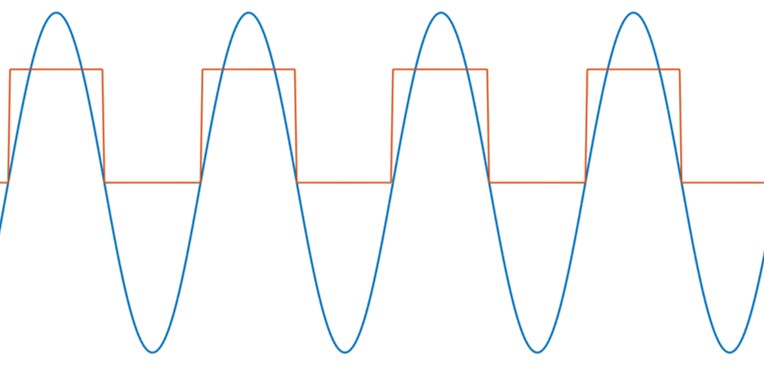
Replicar la tensión de red
Se basa en imitar la forma de la tensión de red para la generación de la señal de referencia. La principal desventaja es que las perturbaciones de la red se propagarán a través del bucle de control, siendo amplificadas cuando el generador actúe en el mismo sentido que las mismas. La implementación estricta de este método no permite el control de la energía reactiva, algo muy importante en los sistemas de generación modernos. A pesar de las desventajas es un método con la suficiente relación «calidad/precio» como para ser defendido en algunas investigaciones como esta: Control technique for single phase inverter photovoltaic system connected to the grid.
PLL básico en la sincronización con redes monofásicas
Se incluye este método más como una introducción que como una propuesta realista. Los PLL son muy utilizados en telecomunicaciones para la modulación y demodulación de señales, así como en el procesamiento de estas. Un PLL (lazo de seguimiento de fase por sus siglas en inglés) es un sistema que genera una señal con la misma fase que la señal de entrada, en este caso la tensión de red. Cuando se intenta utilizar un PLL básico para generar una señal sincronizada con la fase de una red monofásica aparece un problema típico de este sistema: el rizado a doble frecuencia.
Si la tensión de red ug es
\[ u = u_{g} \cdot sen(\omega_{g}t + \theta_{in}\]
Y que la salida del VCO es de la forma:
\[ y= cos(\omega_{pll}t + \theta_{pll} \]
La señal de error ‘e’ valdrá:
\[e = u_{g} \cdot sen(\omega_{g}t + \theta_{in}) \cdot cos(\omega_{pll}t + \theta_{pll})\]
Aplicando el paso de producto a suma
\[\begin{align*}
e = & \, \dfrac{u_{g}}{2} \Bigg[\underbrace{
sen((\omega_{g} – \omega_{pll})t+(\theta_{in}-\theta_{pll}))
}_{\text{Baja frecuencia}}\\
&+\underbrace{
sen((\omega_{g} + \omega_{pll})t+(\theta_{in} + \theta_{pll}))
}_{\text{Alta frecuencia}}\Bigg]
\end{align*}\]
Esta señal de error es capaz de proveer información de la fase de la señal de entrada, pero como ya se adelantó, aparece una componente de alta frecuencia del doble de la frecuencia de entrada que sería conveniente eliminar, lo cual es difícil cuando la señal a seguir tiene una frecuencia baja como la de la red eléctrica.
En la siguiente imagen se muestra la estimación de fase del PLL básico en un sistema monofásico, aunque se podría mejorar ajustando el filtro está claro que no es capaz de seguir correctamente la fase de entrada.
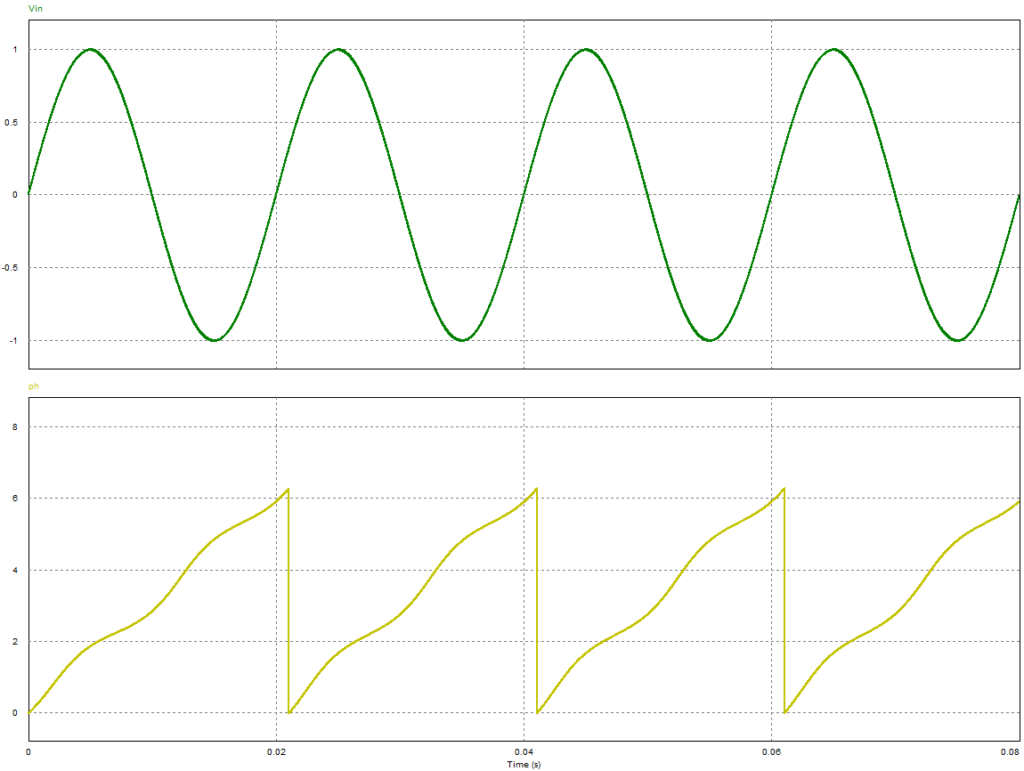
SRF-PLL en la sincronización con redes monofásicas
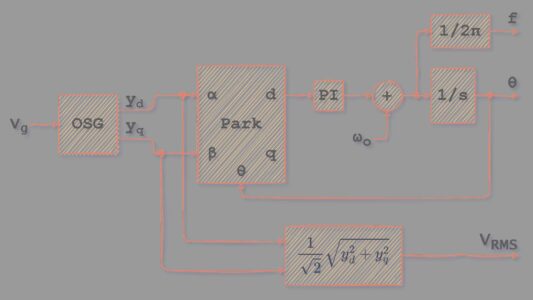
Los SRF-PLL (Synchronous Reference Frame PLL) se basan en crear un sistema de referencia que rota con la misma velocidad angular que el parámetro observado, que en este caso es el fasor de la tensión de red. Mediante este sistema se generan dos señales ortogonales que serán las proyecciones del fasor en el nuevo sistema de referencia, sobre estas señales de frecuencia casi nula, se pueden aplicar métodos de control clásicos para luego deshacer el cambio de sistema de referencia y generar una señal de control en fase, cuadratura o combinación de ambas respecto a la original.
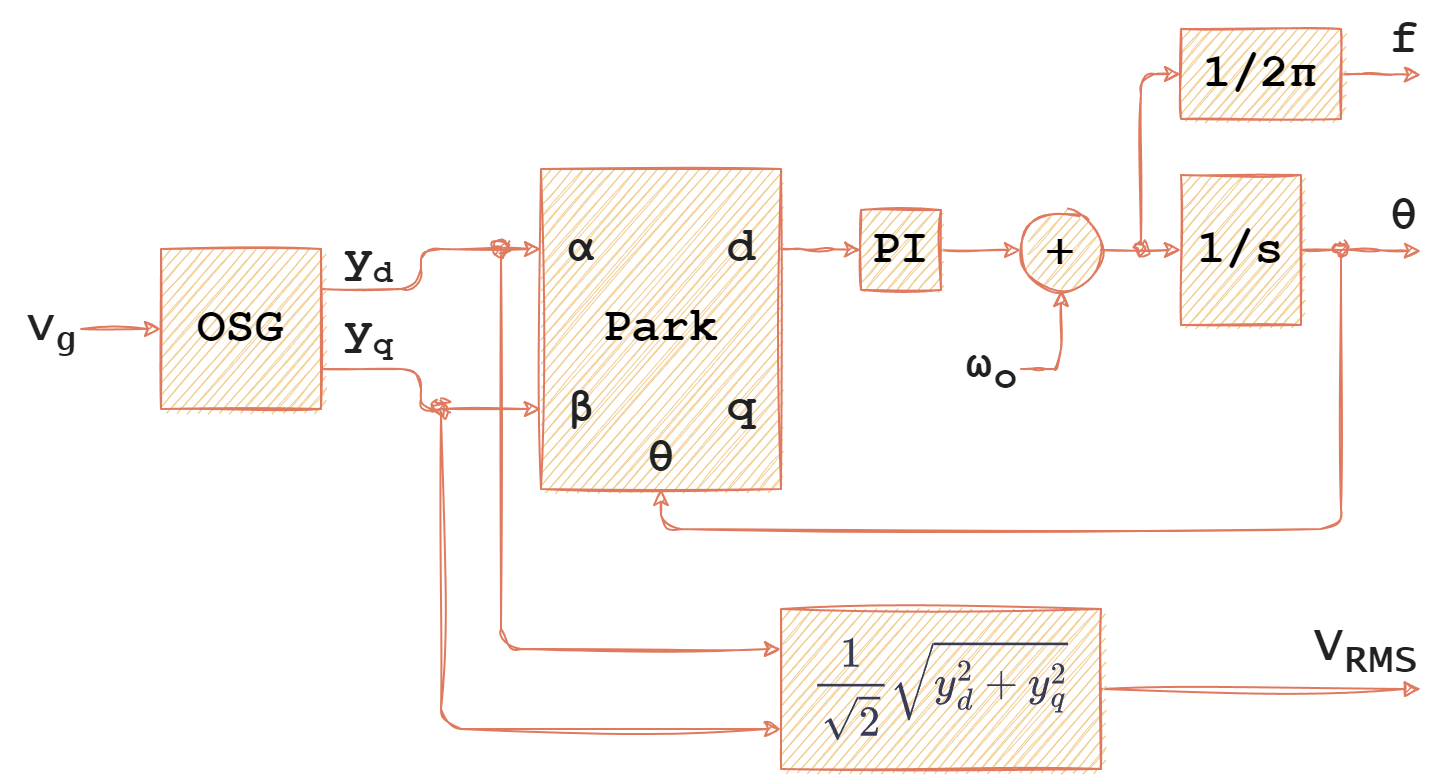
En un sistema monofásico solamente hay una señal de referencia, mientras que la transformada de Park necesita de dos señales de entrada. Debe generarse una señal en cuadratura con la tensión de red para que este sistema funcione. En el esquema anterior esta función la ejerce el OSG (Orthogonal System Generation). Dependiendo del método utilizado para generar esta señal se obtienen distintos resultados.
Cuadratura mediante retardo 90º y filtros de primer orden
Es fácil encontrar este método en distintos medios donde se quiere mostrar o explotar las bondades del SRF-PLL.
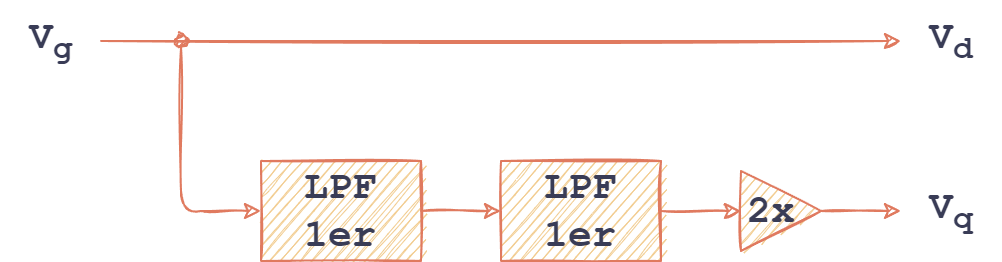
El filtro paso-bajo de primer orden retrasa la señal de entrada 45º para la frecuencia de corte, al colocar dos filtros de este tipo en serie se sumarán los retrasos consiguiendo una señal atenuada pero de -90º, bastará amplificarla para recuperar su magnitud inicial.
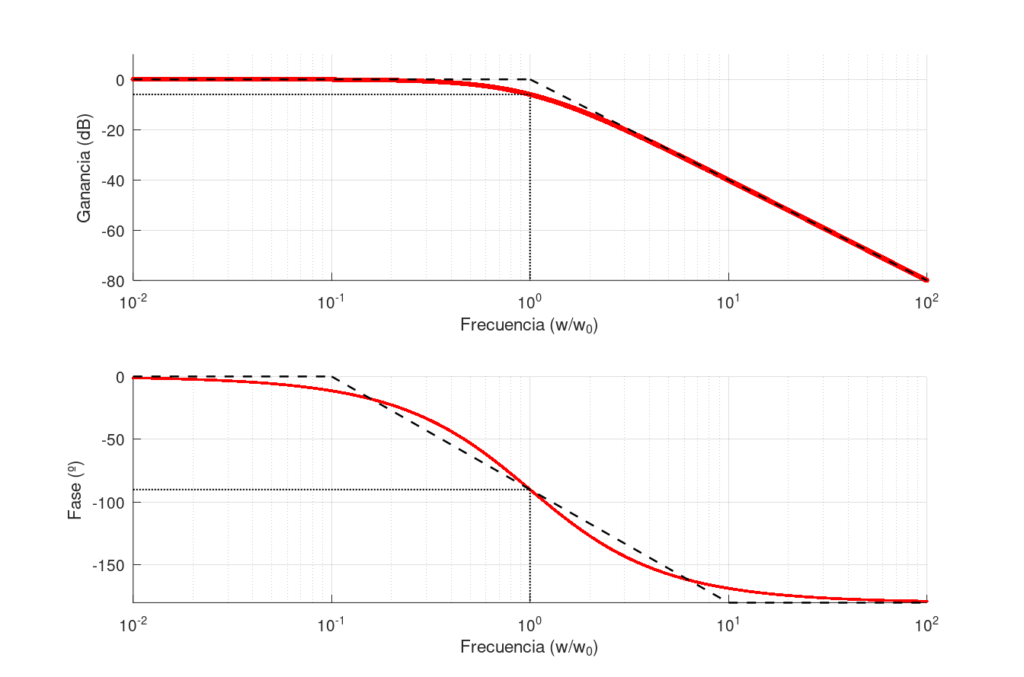
Este sistema exige que la frecuencia de entrada sea siempre y sin excepción igual a la frecuencia de corte de los dos filtros en serie, teniendo en cuenta que la frecuencia de red no es perfectamente constante, del diagrama de Bode se intuye que pequeñas variaciones introducirán errores de varios grados en cada filtro, afectando también a la ganancia. Si a esto se añade la dificultad de construir un filtro que respete sus características ideales, se deduce que no debería utilizarse este sistema más que en el ámbito académico.
Sistema SOGI para generar señal en cuadratura
Mediante el Integrador Generalizado de Segundo Orden (SOGI por sus siglas en inglés), el sistema es capaz de filtrar la señal de entrada y además generar una señal en cuadratura respecto a la misma.
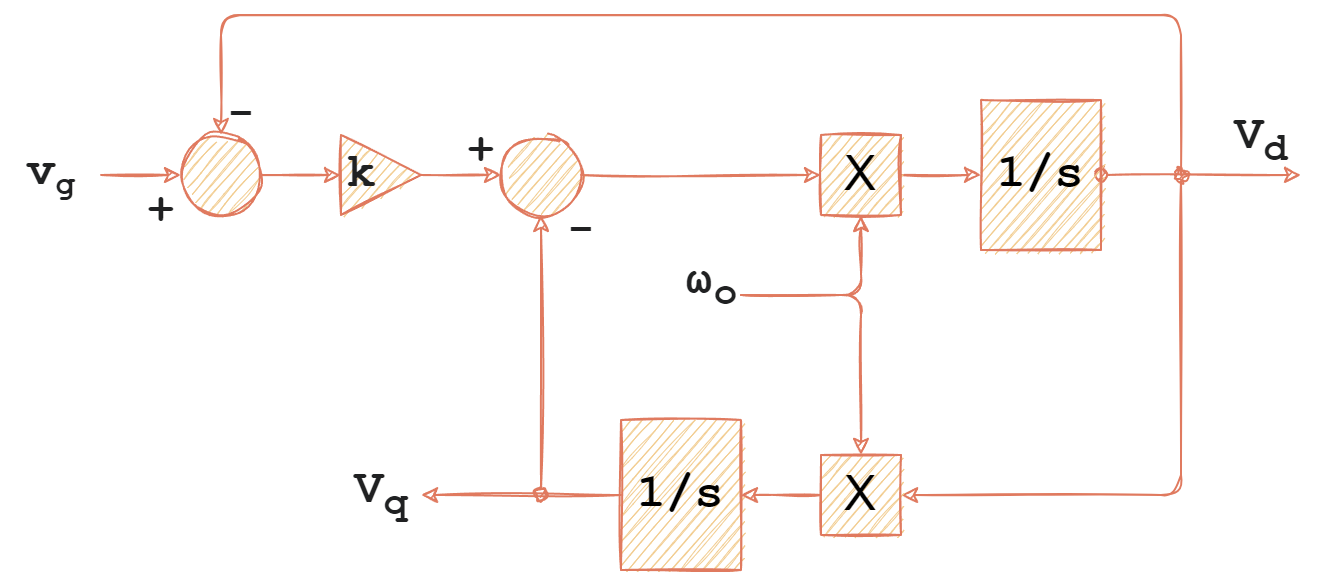
Donde ω0 es la frecuencia de sintonización o resonancia y k un parámetro de ajuste.
El aumento de k provoca que
- El filtrado sea menos selectivo, permitiendo un ancho de banda mayor
- El desplazamiento de fase en el entorno de la frecuencia a la que se ha sintonizado sea más reducido.
- La respuesta tenga una sobrerreacción en un primer momento.
- Se alcance un estado estacionario más rápidamente.
La elección de k es un compromiso entre los 4 parámetros comentados: ancho de banda del filtro, desplazamiento de fase, sobre impulso y tiempo de asentamiento.
El SRF-PLL SOGI se trata en detalle en esta entrada.
EPLL en la sincronización con redes monofásicas
Se trata de derivados del PLL básico que pretenden mejorar las debilidades de este. Un trabajo muy destacable en este sentido es el publicado en Enhanced Phase-Locked Loop Structures for Power and Energy Applications de Masoud Karimi-Ghartema. La complejidad de este tipo de sistemas es elevada, su construcción requiere potencias de cálculo bastante alejadas de sistemas de 8 o 16 bits, al requerir divisiones y operaciones trigonométricas. Por contra se consigue mucha flexibilidad, pudiendo adaptarse a las necesidades de cada sistema.
Desgraciadamente y por derechos de autor no se puede divulgar con total libertad este tipo de trabajos, por tanto, aquí simplemente se hace referencia a su existencia para que el interesado acuda a la fuente para su consulta o estudio.