El cálculo de pérdidas en transistores de potencia es fundamental para el diseño de una refrigeración acorde y la viabilidad de un diseño. Se mostrará un método para estimar las pérdidas de transistores MOSFET tradicionales, SiC y GaN.
Los transistores de potencia presentan pérdidas en forma de calor debido a sus componentes no ideales. Se distinguen dos tipos, las de conducción debidas a la resistencia interna del canal drenador-surtidor y las de conmutación, debidas sobre todo a capacidades parásitas que retrasan el encendido y apagado.
Precisión del cálculo de pérdidas en transistores de potencia
Para realizar estudios sobre un componente suele acudirse al datasheet del fabricante para obtener los datos que sean necesarios. Debe tenerse en cuenta que ninguno de los números o gráficas que aparecen en un datasheet son cerrados y acordes a la realidad. En el proceso de fabricación de un transistor (o de cualquier cosa) nunca existen dos individuos iguales.
La información estadística
Las hojas de características de los componentes se rellenan con datos estadísticos tomados de una gran cantidad de muestras. En algunos casos simplemente representan unos mínimos que cumplirá dicho componente, en otros se especifican rangos en función de otros parámetros como tensiones, intensidades o temperatura.
Los Test Conditions
Test Conditions puede parecer el término estrella de un fabricante, pero es que además de las tolerancias del proceso de fabricación se tienen las no linealidades de los semiconductores. Aunque un transistor podría usarse en cualquier aplicación siempre que se respeten sus áreas de funcionamiento seguras, lo cierto es que se piensan para targets concretos. Estos targets suelen mostrarse en forma de lista bajo títulos como «Applications», «Typical Applications», etc. Los Test Conditions suelen girar en torno a dichos target, por eso, analizar un componente que trabaje en las condiciones típicas de tales aplicaciones debería dar resultados más precisos.
Parámetros reales de un transistor
La lotería del silicio determina el valor final de los parámetros de un componente concreto, por lo que a cualquier estimación o estudio que se haga a partir de un datasheet deben aplicarse márgenes de error suficientes.
En electrónica el prototipo tiene una función más allá de validar una topología o configuración, que es la de despejar dudas que puedan aparecer debido a estas tolerancias.
Para ilustrar como obtener los datos para el cálculo de pérdidas en transistores de potencia se utilizará como ejemplo el STF33N60DM6, sin más intencionalidad que ilustrar y aclarar la información que se expone. La inmensa mayoría de hojas de características que pueden encontrarse presentan los datos de forma muy parecida.
Pérdidas por conducción
Causadas por la resistencia entre drenador y surtidor RDS(on). El valor de esta resistencia está dada directamente por el fabricante, dicha resistencia varía en función de la tensión puerta-surtidor (VGS), de la temperatura y de la corriente que circula por el transistor. En la siguiente imagen pueden verse un par de gráficas de cómo se comporta esta resistencia en función de la corriente y la temperatura.

A pesar de todo, estas pérdidas son las más sencillas e intuitivas de calcular, pues son iguales a las de cualquier resistencia discreta:
\[P_{Ron}=I_d^2·R_{DS(on)}\]
Pérdidas por conmutación
Debido a las capacidades parásitas en la puerta del transistor el encendido y apagado no será instantáneo, presentando ciertos retardos desde que se efectúan las órdenes hasta que comienzan los transitorios. Por otro lado, la carga y descarga de estas capacidades parásitas provocarán que el transistor no pase de abierto a cerrado (o viceversa) inmediatamente. En dichas transiciones se tienen incrementos y decrementos de tensión e intensidad entre drenador y fuente, lo que provocará importantes pérdidas en forma de calor.

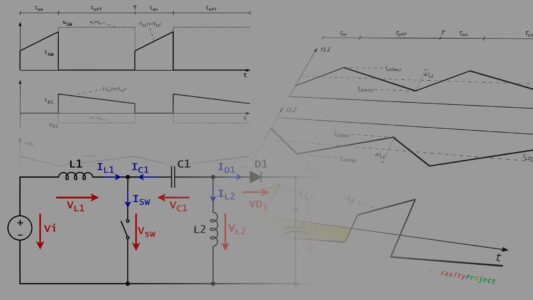
Considerando una carga inductiva se establecen tres etapas para el encendido y otras tres para el apagado, como se ve en la imagen.

Mientras que los valores td(on), tri, td(off) y tfi se obtienen directamente del datasheet, tfv y trv deben ser calculados al depender de las condiciones de trabajo.

Los valores td(on), tri, td(off) y tfi, estarían estimados para las condiciones que indica el fabricante en Test conditions.
Cálculo de tfv
Para el cálculo de tfv en el encendido del transistor (paso de corte a saturación), se considera el siguiente circuito equivalente.

Dónde
\[\left.
\begin{array}{rcl}
V_{gg}&=&i_g·R_g+V_{GS}
\\ V_{DS}&=&V_{DG}+V_{GS}
\\ i_g&=&-C_{gd}\frac{dV_{DG}}{dt}
\end{array}
\right\}\]
Durante el encendido, mientras se produce la caída de tensión entre colector y surtidor, la tensión entre puerta y surtidor VGS se denominará VGS*, cuyo valor se enseñará a obtener más adelante.
Derivando la segunda ecuación del sistema anterior respecto del tiempo
\[\frac{V_{DS}}{dt}=\frac{V_{DG}}{dt}+\frac{V_{GS}^*}{dt}\]
Como VGS es constante su derivada será nula:
\[V_{GS}=cte \rightarrow \frac{dV_{GS}^*}{dt}=0\]
Operando en el sistema, sustituyendo la tercera ecuación en la primera y junto a la derivada anterior se tiene
\[V_{gg}=-C_{gd}\frac{dV_{DS}}{dt}R_g+V_{GS}\]
\[\frac{dV_{DS}}{dt}=\frac{V_{gg}-V_{GS}^*}{-C_{gd}R_g}\]
Esta última ecuación describe la tasa de variación de tensión entre drenador y surtidor por unidad de tiempo. Al conocer el incremento de tensión que se producirá, se puede obtener el tiempo que tardará en producirse, esto es tfv.
\[t_{fv}=\frac{dV_{DS}}{\frac{dV_{DS}}{dt}}=\frac{\Delta V_{DS}}{\frac{\Delta V_{DS}}{dt}}\]
El incremento de tensión que se producirá entre drenador y surtidor será desde la tensión con el transistor en corte Ve hasta la caída de tensión producida por la resistencia interna RDS(on):
\[\Delta V_{DS}=I_dR_{DS(on)}-V_e\]
Por tanto
\[t_{fv}=\frac{I_dR_{DS(on)}-V_e}{\frac{V_{gg}-V_{GS}^*}{-C_{gd}R_g}}\]
Queda obtener VGS*, este dato puede calcularse de la curva de transferencia dada por el fabricante de la siguiente forma
\[I_d=G_m\left(V_{GS}^*-V_{TH}\right)\]
Por ahora simplemente se despeja VGS*, ya que los valores Gm y VTH se enseñará a obtenerlos del datasheet más adelante.
Finalmente se tiene que tfv es
\[t_{fv}=\frac{I_dR_{DS(on)}-V_e}{\frac{V_{gg}-\frac{I_d}{G_m} – V_{TH}}{-C_{gd}R_g}}\]
Cálculo de trv
Se sigue un planteamiento similar al de tfv, partiendo del siguiente circuito equivalente para el apagado del transistor. En él la tensión drenador-surtidor se eleva mientras la intensidad aún no ha comenzado a reducirse.

\[\left.
\begin{array}{rcl}
V_{GS}&=&-i_g·R_g
\\ i_g&=&-C_{gd}\frac{dV_{DG}}{dt}
\end{array}
\right\}\]
Derivando la primera ecuación y sustituyendo en la segunda
\[ \frac{dV_{DS}}{dt}=\frac{V_{GS}^*}{C_{gd}R_g}\]
Como con tfv se tiene
\[t_{rv}=\frac{\Delta V_{DS}}{\frac{\Delta V_{DS}}{dt}}=\frac{I_dR_{DS(on)}-V_e}{\frac{\frac{I_d}{G_m} + V_{TH}}{C_{gd}R_g}}\]
Obtener el valor de Cgd,
Los datos específicos del transistor para utilizar las ecuaciones anteriores se obtienen de forma directa o indirecta en el datasheet, donde se puede encontrar una imagen como la siguiente

En ella el valor de Cgd corresponde a CRSS, la cual varía en función de la tensión drenador surtidor, que aquí se ha llamado Ve. Por ejemplo, para una tensión Ve de 100V se tendría una capacidad Cgd de unos 3pF.
Estimar Gm y VTH
A partir de la curva de transferencia facilitada por el fabricante se obtienen estos parámetros.
VTH se toma de forma aproximada por observación directa, se encuentra cerca del punto de inflexión donde la corriente por el drenador comienza a dispararse.

Gm es más difícil conseguirlo, debe tomarse la parte de la curva en la zona de trabajo y estimarse la pendiente de dicha recta. En la imagen anterior se ha supuesto una corriente de funcionamiento de 15A, se ha trazado una recta sobre dicha curva y se han estimado los valores sobre los que descansan los extremos.
Con ello se tiene aproximadamente que
\[G_m=\frac{\Delta Y}{\Delta X}\approx\frac{15}{0,75} \approx 20 \]
Cálculo de pérdidas en transistores de potencia
Las pérdidas totales serán la suma de las debidas a conducción y a conmutación.
Para las pérdidas por conducción se tendrá en cuenta el tiempo que el transistor se encuentra encendido durante un segundo, si la aplicación trabaja a una frecuencia f se tendría que
\[ P_{Ron}=I_d^2·R_{DS(on)}·t_{on}·f \:\:(W)\]
Las pérdidas por conmutación deben tener en cuenta cuatro periodos de tiempo distintos, tri, tfv para el encendido y trv y tfi para el apagado.

\[P_{t_{ri}}=V_e \left(\int_{0}^{t_{ri}} \frac{i_D}{t_{ri}}t·dt\right)f = V_e\frac{i_Dt_{ri}}{2}·f \:\:(W)\]
\[P_{t_{fv}}=\frac{(V_e-i_DR_{DS(ON)})t_{fv}}{2}i_D·f \:\:(W)\]

\[P_{t_{rv}}=\frac{(V_e-i_DR_{DS(ON)})t_{rv}}{2}i_D·f \:\:(W)\]
\[P_{t_{fi}}= V_e\frac{i_Dt_{fi}}{2}·f \:\:(W)\]
Finalmente
\[P_{TOTAL}=\underbrace{P_{Ron}}_{\text{Conducción}}+\underbrace{P_{t_{ri}}+P_{t_{fv}}+P_{t_{rv}}+P_{t_{fi}}}_{\text{Conmutación}}\]
Dependiendo de la aplicación podrían ignorarse las pérdidas por conmutación si, por ejemplo, el transistor trabaja durante largos periodos de tiempo sin cambiar su estado.
En el caso de aplicaciones donde existan muchos ciclos de encendido y apagado como convertidores de potencia conmutados, una buena práctica será la de no sumar ambas pérdidas. De esta forma podrá analizarse el uso de una frecuencia de conmutación más o menos elevada, llegando a un compromiso entre el tamaño de los inductores y las pérdidas que se consideren admisibles.
Bibliografía
Electrónica de Potencia. Componentes topologías y equipos. JUAN ANDRES GUALDA GIL, SALVADOR MARTINEZ GARCIA. Parainfo